최다득표로 승자 가리는 선거제도…두 개의 주요 정당만 남게 돼

뒤베르제의 법칙과 전략적 투표

한국이나 미국처럼 ‘최다득표제’로 승자를 가리는 선거제도를 운영하는 많은 국가에서는 대체로 양당체제라는 정치시장의 구조적 특성이 나타난다. 이런 정치적 현상을 가장 잘 설명하는 공공선택학적 이론이 ‘뒤베르제의 법칙’이다.

이 법칙에 따르면 최다득표제를 선거제도로 채택하는 국가에서는 지역별로 고르게 지지도를 보이기는 소수 정당은 어떤 의석도 얻을 수 없고, 시간이 지남에 따라 정치적 지지 기반을 상실한다. 따라서 최다득표제하에서는 소수 정당을 찾아볼 수 없게 되고 두 개의 주요 정당만이 남는다고 뒤베르제의 법칙은 예견하고 있다.

1954년 프랑스 정치학자 모리스 뒤베르제(사진)가 제시한 이 법칙은 국민이 전략적으로 투표한다는 것을 전제로 하고 있다. 전략적 투표란 개념은 유권자가 최다득표제하에서 어떻게 투표하는지 생각해보면 쉽게 알 수 있다. 우선 A, B, C 세 개의 정당이 경쟁하고 있고 유권자는 여론조사와 지난 선거 결과를 토대로 A, B, C 순서로 승리 확률이 높다고 판단한다고 가정해 보자. 이 유권자가 행사하는 한 표가 캐스팅 보트가 되기 위해서는 A와 B가 동등한 득표율을 얻어야 하며 B와 C의 승리 확률이 아주 근소한 차이를 보이지 않는 한 A와 B가 동등한 득표율을 얻을 확률이 A와 C가 동등한 득표율을 얻을 확률보다 항상 크다. 즉, 의석을 얻기 위한 유효경쟁은 A와 B라는 상위 두 개의 정당 간에 벌어진다.

이는 유권자가 선거 결과에 영향력을 발휘하기 위해서는 A나 B 중 자신이 좀 더 선호하는 정당에 표를 줘야 하며, C에 투표한다면 이 유권자가 행사한 표는 사표(死票)로 전락한다는 것을 의미한다. 즉, 다수득표제하에서 합리적 유권자는 승리 확률이 높은 상위 두 개의 정당을 선호하고 소수 정당은 고려 대상에서 제외해 소수 정당인 C는 정치시장에서 존재 가치를 잃는다.

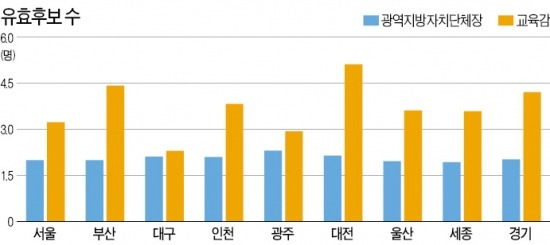
이런 합리적 유권자의 전략적 투표 분석은 최다득표제하에서 두 개의 정당이 남게 된다는 뒤베르제의 법칙을 두 명 이상의 당선자를 선출하는 선거제도하에서는 세 개 이상의 정당이 존재한다는 ‘뒤베르제의 가설’로 발전시켰으며, 이 가설은 비례대표제 하에서 다수의 정당이 존재하는 설명으로도 사용되고 있다.

전략적 투표 분석을 통해 두 명 이상의 당선자를 뽑는 선거제도하에서 세 개 이상의 정당이 존재하는 이유 또한 이전의 경우와 같이 쉽게 설명할 수 있다. 우선 A, B, C, D 네 개의 정당이 한 선거구에서 두 개의 의석을 얻기 위해 경쟁하며 A, B, C, D 순서로 유권자가 승리 확률을 판단하고 있다고 가정해 보자. 그렇다면 A는 거의 확실히 의석을 확보할 것이며, 경쟁은 한계 의석인 두 번째 의석을 차지하기 위한 B와 C 간에 이뤄질 것이다. 따라서 선거 결과에 영향력을 발휘하고 자신의 표가 사표로 전락하는 것을 방지하고자 합리적 유권자는 전략적으로 B나 C 중 자신이 선호하는 정당에 한 표를 행사할 것이다. 즉, 소수 정당인 D는 전략적 투표를 하는 합리적 유권자의 고려 대상에서 제외되며 퇴출되는 수순을 밟게 된다.

전략적 투표하의 이런 논리는 정당 간의 유효경쟁이 n개의 의석을 가리는 경우 한계 의석인 n번째 의석을 차지하려는 n번째와 n+1번째 지지를 받는 정당 간에 벌어지며 n+2번째로 지지받는 정당부터는 정치시장에서 퇴출된다는 것을 의미한다.