블랙홀 운명 밝혀 노벨물리학상 수상한 펜로즈 우주 시공간의 전체 기하학적 구조에서 파악

과학 이야기
과학과 놀자 (23) 펜로즈의 삼각형과 블랙홀 - 부분과 전체

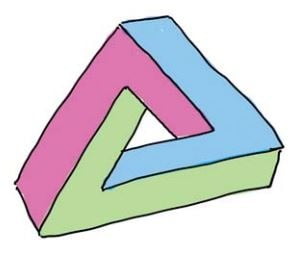
<그림1> 펜로즈의 삼각형. 부분을 보면 가능해 보이지만, 전체를 보면 현실에서 구현이 불가능한 삼각형이다.

2020년 노벨물리학상 수상자인 로저 펜로즈는 정신과 의사인 아버지와 함께 '펜로즈의 삼각형'<그림1>으로 알려진 비현실적인 도형을 디자인했다. 이 도형들은 상대론을 그림에 담고자 했던 화가 에셔(Escher)와의 교감을 통해 발전해갔다. 펜로즈의 삼각형과 에셔의 판화 '폭포(Waterfall)'<그림2>는 부분을 보면 현실적으로 가능하지만 전체를 보면 구현이 불가능하다. 펜로즈는 이런 불가능한 도형의 기하학적 연구를 확대해 블랙 홀 형성이 우리 우주에서 피할 수 없는 운명임을 밝혔다.

아인슈타인도 부정한 블랙홀의 존재

<그림2> M. C. 에셔의 판화 ‘폭포’(1961). 물이 수로를 통해 아래로 흐르지만 어느새 폭포의 위에 도달하는 것으로 그려져 있다. 에셔재단 홈페이지(mcescher.com)

아인슈타인의 일반상대론이 1915년 발표된 직후, 1916년 슈바르츠실트는 ‘구대칭 구조의 블랙홀 해(解)’를 발견했다. 이 해에 의하면 빛도 빠져 나오지 못하는 영역인 사건의 지평선이 존재한다. 그런데 블랙홀 해는 사건의 지평선과 중심에서 무한대로 발산하는 성질을 가지고 있어서 논란의 대상이 됐다. 아인슈타인은 블랙홀의 존재를 부정했고 계산을 통해 블랙홀이 현실적으로 불가능함을 보였다. 상대론으로 우주 시공간의 인식을 바꾼 아인슈타인이지만, 양자역학에 이어 블랙홀의 존재까지 부정한 것이다.

그런데, 아인슈타인의 계산은 몇 가지 잘못된 가정에서 출발했다. 별이 블랙홀로 수축하지 않고, 유한한 밀도를 가진 평형 상태에서 멈출 것이라고 가정한 것이다. 슈바르츠실트 해에 의하면 태양이 반경 3㎞ 이내로 압축되면 블랙홀이 되고, 지구가 반경 9㎜ 이내로 압축되면 블랙홀이 되는데, 당시 상식으로는 상상할 수 없는 현상이었기 때문이다. 압축되기 전에 다른 안정된 상태에서 멈추는 것이 훨씬 자연스러워 보였을 것이다.

펜로즈, 무한한 우주를 작은 도형 속에 담다

1963년 은하 중심의 활동성 은하핵이 발견되고 회전하는 블랙홀의 해가 발견되면서 블랙홀에 대한 인식이 변하게 된다. 이 인식 변화에 결정적인 기여를 한 과학자가 이번 노벨상 수상자 펜로즈다. 펜로즈에 의해 블랙홀 연구의 흐름이 바뀌게 된다.

블랙홀 운명 밝혀 노벨물리학상 수상한 펜로즈, 우주 시공간의 전체 기하학적 구조에서 파악

은하 중심에 있는 활동성 은하핵이 회전하는 블랙홀일 가능성이 제시됐고, 이 소식을 접한 펜로즈는 기존 연구와는 다른 관점에서 블랙홀을 연구했다. 기존 연구에서는 특이점, 사건의 지평선, 들어가는 빛과 입자의 운동 등과 같이 부분적인 문제에 집중했다. 그런데 펜로즈는 블랙홀 형성 가능성을 시공간의 전체 기하학적 구조에서 파악한 것이다. 이를 위해, 무한한 우주를 작은 도형 속에 담은 ‘펜로즈 다이어그램(Penrose diagram)’<그림3>을 고안했다. 펜로즈의 삼각형처럼, 부분을 통해 파악할 수 없는, 전체를 통해서만 이해할 수 있는 블랙홀의 성질이 있음을 인식한 것이다. 펜로즈 다이어그램에서 빛은 대각선으로 이동한다.

펜로즈는 회전하는 블랙홀의 기하학적 구조 연구를 통해 블랙홀 회전에너지의 일부를 직접 빼낼 수 있다는 사실도 발견했다. 펜로즈 프로세스(Penrose process)로 이름 붙여진 이 과정은 감마선 폭발로 알려진 천체 현상의 주요 메커니즘으로도 주목받고 있다. 감마선 폭발은 태양이 평생 방출하는 에너지에 해당하는 큰 에너지를 수초에서 수분 이내에 감마선으로 방출하는 천체 현상으로 현재까지 수천 개가 발견됐다.

무한한 길이를 유한한 변수로 표현하는 방법은 막대의 그림자를 생각하면 이해할 수 있다. 햇빛이 수직으로 쬐이는 경우, 그림자 길이가 같도록 막대의 각도와 길이를 조절하면 어떻게 될까. 막대의 각도가 수직에 가까워지면 길이는 무한대로 늘어나야 한다. 이와 같이 무한한 길이를 90도 이내의 각도로 나타낼 수 있다. 이때 막대의 길이와 각도는 1 대 1로 대응된다.

부분과 전체

펜로즈는 부분이 아닌 전체를 바라봄으로써 블랙홀 연구의 새로운 지평을 개척했다. 블랙홀 생성이 우리 우주의 필연적 결과임을 밝힌 것이다. 은하 중심의 거대 블랙홀뿐 아니라 항성질량 블랙홀이 관측된 현재, 블랙홀은 수학적인 해가 아니라 현실이 됐다. 그리고 블랙홀 중심의 특이점 또한 인류가 해결해야 할 현실 문제가 됐다. 다시 한 번 부분이 아닌 전체 연구를 통해 우주의 신비가 밝혀지기를 기대해 본다.

√ 기억해주세요

이창환 부산대 물리학과 교수

대부분의 은하 중심에 거대 블랙홀이 존재하는 것으로 추정된다. 우리 은하 중심에도 태양 질량의 수백만 배 질량을 가진 거대 블랙홀이 존재한다. 2020년 노벨물리학상은 우리 은하 중심의 블랙홀을 관측한 업적에 수여됐다. 2019년에는 5500만 광년 떨어진 M87은하 중심에 있는 블랙홀 그림자 촬영에 성공했다. 이 블랙홀의 질량은 태양의 65억 배로 추정된다. 2002년 노벨물리학상을 수상한 엑스선 관측에서는 현재까지 태양의 30배 이하 질량을 가진 블랙홀이 수십 개 발견됐다. 그런데, 2017년 노벨물리학상을 수상한 중력파 연구에서는 (2015년 중력파 최초 검출 이후 현재까지) 태양의 30배보다 큰 질량을 가진 수십 개의 블랙홀이 새로 발견됐다. 특히, 최근 태양 질량의 150배 질량을 가진 블랙홀이 중력파로 발견돼 블랙홀 연구에 새로운 활력을 불어넣고 있다.